蜗牛扑克allnew官网,蜗牛扑克allnewpoker官网,蜗牛扑克allnewpoker国际场,allnewpoker官网下载,蜗牛扑克网站,蜗牛扑克下载——(allnewpuke.com)
作为对这个博弈游戏的简单介绍,我们来考虑一种最简单的博弈游戏,也就是奇数偶数游戏。两个玩家在玩这个游戏。两个人都单手握拳,手里可以放1枚或者不放硬币,两人互相看不到对手手里是否有硬币。根据事先的约定,如果硬币总数是偶数的话那么其中一个玩家(玩家A)赢得一个单位,如果硬币总数是奇数的话另一个玩家(玩家B)赢得一个单位。

接下来我们要在这个简单的游戏中介绍的是收益矩阵。玩家B的策略从左到右列出,而玩家A的策略从上到下列出。而一旦双方策略被揭示以后,在图表中找出他们相对应的每个牌手的收益(A的收益,B的收益)。

在这些博弈中会有一些有趣的性质。一些博弈,例如奇数偶数游戏和无抽水的扑克游戏,我们称之为常和博弈。所有玩家的收益总和是一个常数。在扑克中,这个常数恰巧为0,所以通常我们也称之为零和博弈。所有的常和博弈可以通过适当地调整收益来变换为零和博弈。
第二个博弈中的重要性质是,一个博弈或者是序贯博弈,或者是同时博弈。例如,在奇数偶数博弈中,这个游戏是一个同时博弈。而在一个棋类游戏中,博弈是序贯的;一个玩家先行动后,另一个玩家才行动。在某种程度上,我们可以将所有游戏都归为同时博弈,只要通过让所有的玩家在博弈之前定义他们完整的策略(即整个博弈树)即可。然而,讨论序贯博弈与同时博弈的区别仍然是有用的,因为这可以让我们对混合策略有进一步的认识(不仅仅在于某个时点)。
关于博弈的另一个性质在于博弈中存在的隐含信息。隐含信息指的是博弈中一个玩家了解的但却不被另一个玩家知晓的信息。首先考虑一个博弈,比方说下棋。在这个游戏中,整个棋局的情况在任何时点对任意一个玩家都是有效的,并且这个游戏是完全确定的;也就是说,一个玩家或者电脑如果有足够的计算能力的话,可以模拟出完整的博弈树并且找到每一步的最优解。这是一个没有隐含信息的博弈的例子。西洋双陆棋是另一个没有隐含信息的博弈的例子,不过它却不是完全确定的。每一次骰子掷出不同的点数时,博弈树变化了,但是概率选择进程的机制对每个玩家都是知晓的。因此,在这个例子中,即使因为随机性使得每个玩家都不能通过完美打法确保胜利,但这里仍然没有隐含信息;记住,没有隐含信息指的是,没有任何信息是一个玩家知道而另一个玩家不知道的。
而扑克,从另一方面来说,是一个非常依赖于隐含信息的游戏。每位牌手知道他自己的手牌,而对他对手手牌的认知将会是一个巨大的恩惠。因此,扑克的目标就是通过从隐含信息中获取优势来攫取价值。从博弈论的角度来看,博弈中有关隐藏信息的最重要的一点就是他们的最佳策略可以包含混合策略。混合策略指的是在单个情形中包含两个或者更多可能的决策的情形。举个例子,“在满员桌拿到AA时候,一半的情况下直接加注,在一半的情况下溜入——加注”就是一个混合策略的例子。只有那些或者包含隐含信息或者连续博弈博弈可能包含混合最优策略。
在运用博弈理论学习扑克的过程中,两人零和博弈游戏(例如奇数偶数游戏)通常是最重要的和最有趣的。在两人零和博弈中,只有两个玩家会有收益,并且这些收益的和一定是0;也就是说,玩家A失去的,就是玩家B赢得的,反之亦然。这些关于最优策略的观点仅仅在两人零和博弈中适用。
我们可以讨论一个策略配对;也就是,一个关于一个玩家的策略和另一个玩家策略的策略组合。对于一个两人零和博弈游戏,一个策略配对是最优的意味着任何一个玩家不能通过单边地调整策略来改进他们的期望收益。一个策略如果是一个玩家的最优策略的话,那这个策略一定是最优策略配对的一部分。
想象你正在和一个超级玩家对局。我们称这个超级对手为天选之人。这个天选之人总是知道你的策略,并且总是针对这个策略采取最大剥削策略。如果你调整你的策略,这个对手会立马调整以做出反击,即总是能对你采用最优的剥削策略。
一对最优的策略包含两种最大程度剥削双方的策略。
请注意,这里的“最优”是有详细定义的——许多地方会用到这个词,有些时候会有各种各样的定义和解释。我们这里只是在讨论策略的时候用最狭窄的定义。
在零和双人游戏和其他类型的游戏中,不定和或者多人游戏,我们始终满足一个条件,也就是当没有人可以通过任何的行动来提高他的期望值时,此时双方满足这个条件下的策略被称为纳什均衡。所有具有有限收益表的多人游戏可以被证明至少包含一个均衡点;有些游戏含有多个均衡点。实际上,一些游戏正是因为包含了许多均衡点而难以分析。我们会在第五部分重新回顾。
数学告诉我们,一个双人零和游戏的最优策略有以下性质:
· 只要允许混合策略(也就是说,每个玩家可以使用比如60%的时候进行X,剩下的40%进行Y),那么最优策略始终存在
· 引出的一个推论是,如果一个最优策略包含混合策略,那么双方可用策略的期望在面对对手策略时相同。因此,扑克中的最优策略不包括“促销策略”,即通过牺牲一定期望来欺骗对手。如果一手牌有不同的打法,那么每种打法都有相同的期望值。如果不是这样,那么玩家可以简单的把所有低期望的打法转成高期望的打法,来实现单方面的进步。
常见的是,特别在一些非常简单的游戏,最优策略往往就是那些保证零期望的策略。这是因为简单的游戏经常是完全对称的;这样的话,我们在使用最优策略的时候,最优策略势必导致零期望,因为对手也可以简单地使用最优策略应对。
回顾奇数偶数游戏,很清楚的是,玩家A的目的是应对玩家B的策略。双方可以用非常剥削的猜测玩法,试图在思路上领先对手;如果那样的话,谁能多想一步就可以取得优势。然而,还有另外一个选择。假如B觉得在猜测上不如A,那么他可以选择去最优化地玩这个游戏。其中方法之一就是找到一个针对其他所有策略的策略应用,并且最大化胜率。
B可以使用混合策略,比如在X%的时候,不放硬币,而在剩下的1-X%的时候放硬币。显然单纯策略就是给其中一个选项100%的权重。
我们可以直接计算A应对策略的期望值,但是我们应该知道通过之前剥削策略,强敌会完美地通过一个单纯策略来剥削B。比如B在超过50%的时候不放硬币,那么强敌会永远不放硬币。而如果B在超过50%的情况下放硬币,那么对手会永远放硬币。
通过公式1.11,B不放硬币的期望>0.5是:
< B, x > 0.5 > = (-1) (x) + (1) (1-x)
< B, x > 0.5 > = 1 – 2x
放硬币期望>0.5是:
< B, x <0.5 > = (-1) (x) + (1) (1-x)
< B, x <0.5 > = 2x – 1
我们可以看到在两种情况下,期望都是负数。当x > 0.5, 1 – 2x是负数, 而当 x < 0.5, 2x – 1也是负数。
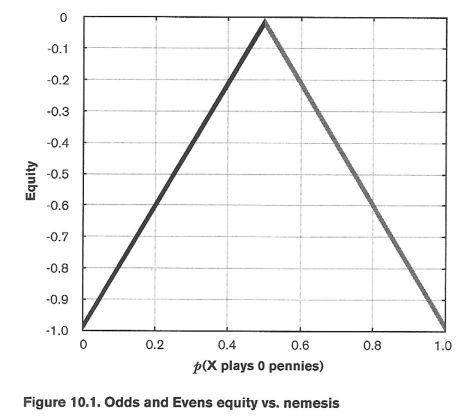
在x = 0.5的时候,强敌可以做任何动作来实现同样的胜率。
< 强敌,不放硬币 > = (-1) (0.5) + (1) (0.5)
< 强敌,不放硬币 > = 0
< 强敌,放硬币 > = (-1) (0.5) + (1) (0.5)
< 强敌,放硬币 > = 0
这也是B在面对强敌时可以获得的最大期望。因此,x = 0.5是B的最优策略。B可以通过50%的随机选择放还是不放硬币,来保证自己有零期望。为了实现这个,他可以使用任何外部的随机;比如扔个骰子,扔个硬币,或者是辐射衰减的量子测量,如果他有足够的需求不被剥削。
畅玩线上德州扑克,只需简单步骤就能在Bodog博狗畅玩扑克,
博狗扑克官方网址 博狗扑克网址:http://www.bogoupoker.com
好消息 蜗牛扑克GG扑克室-全新德扑玩法“极速&现金桌”上线!
全天24小时随机将掉落现金红包至牌局底池或玩家余额!快体验吧
蜗牛扑克优惠提供30%超高额返水
蜗牛扑克官方网址:www.allnew366.com
蜗牛扑克网址发布页:www.allnewpuke.com
蜗牛娱乐官网:www.allnewbet8.com
蜗牛扑克GG官网:www.ggallnew.com
扑克反水-德州扑克反水-博狗扑克反水-蜗牛扑克反水-扑克之星反水-联众扑克反水-天龙扑克反水












