Modern Poker Theory
现代扑克理论
胜率/底池权益(Eq)
底池权益(Equity)是你在牌局某个时间点取决于获胜或打平机会的底池份额。胜率(Equity)是如果没有后续下注且所有牌发出后平均而言你将多频繁地赢得底池。胜率可以用使用一种胜率计算器轻易算出。
译注:Equity在扑克中是一个多义词,有时指我们底牌的获胜机率,译者译做胜率,有时指根据我们的胜率我们应该占有的底池份额(底池的百分之多少),译者译做底池权益。
以下是两个你可以免费访问的资源:
pokerstrategy.com/poker-software-tools/equilab-holdem
propokertools.com/simulations
如我们接下来将看到的,考虑胜率有各种各样的方式。
底牌对抗底牌的胜率
底牌不能根据它们的牌力排名(rank),因为每手牌的牌力是相对于对手的底牌或范围而言的。
让我们使用胜率来分析下列三手牌,并试着判断哪手牌最强(表格2)。

表4:底牌对抗底牌的胜率
如我们所见,AKo的胜率高于JTs,而22的胜率高于AKo。你可能通过逻辑推理认为22必定胜率高于JTs。然而,事实证明JTs其实胜率高于22。因此,我们没有任何办法给这三手牌排名。
即使在真空情况下底牌对抗底牌的胜率无法用来给底牌排名,但它可以帮助我们理解底牌相互对抗的情况。
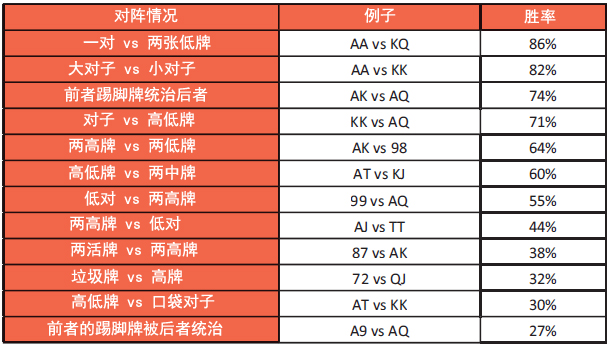
表5:常见对阵情况的翻前胜率
底牌对抗范围的胜率
当你打牌时,你永远无法确切知道对手的两张底牌是什么。但是,你可以基于他的行动给他分配一个范围,然后计算你对抗那个范围的胜率。
牌例
牌局类型:100美元买入网络三人SNG比赛
有效筹码量:按钮玩家30BB,小盲玩家10BB,大盲玩家20BB
牌手数量:3人(无前注)
翻前:按钮玩家弃牌。小盲玩家是一名紧手,他全压10BB。你在大盲位置拿着Q♣ T♣,必须决定是跟注还是弃牌。
我们使用底池赔率公式:

如果你的牌可以在至少45%的时候获胜(即具有至少45%胜率),跟注将是有利可图的。因为你知道对手是一名紧手,你可以给他分配一个比标准牌手或松手更紧的范围(底牌范围6)。

底牌范围6:小盲玩家的率先全压范围(10BB)
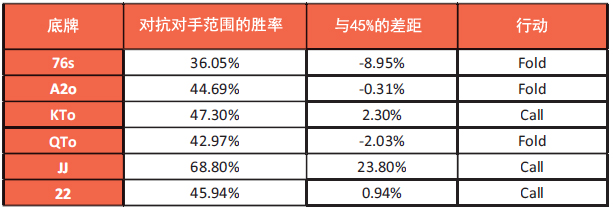
表6:各种底牌的胜率及它们相比45%的胜率差距
你的牌Q♣ T♣ 对抗这个范围没有足够的胜率(你将在43%的时候获胜,但你需要在45%的时候获胜),因此你应该弃牌。
范围对抗范围的胜率
范围对抗范围的胜率在你考虑每个牌手如何受公共牌影响的翻后场合很有用。
牌例
牌局类型:109美元买入网络9人MTT比赛
有效筹码量:40BB
牌手数量:9人(12.5%前注)
翻前:前面玩家都弃牌,你在CO位置拿着A♦ A♣,你加注到2.25BB。后面玩家弃牌,轮到大盲位置的强硬常客玩家行动。你估计他对抗CO位置加注采用下面的策略防守(底牌范围7)。
你用一个约31.2%起手牌的标准CO位置率先加注范围加注(底牌范围8)。
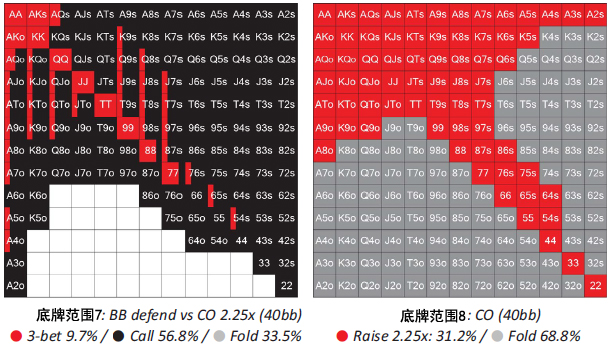
CO玩家的31.2%加注范围对抗BB玩家56.8%跟注范围的胜率分布如下(表7)。
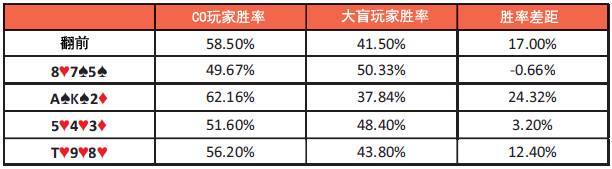
表7:在各种翻牌面的胜率分布
比较范围对抗范围的胜率,我们可以看出翻前Hero具有优势,但胜率分布将根据翻牌结构而改变。理解胜率如何在不同公共牌面变化对于Hero很重要,因为那会对牌局的游戏方式产生显著影响。我们来考虑一个翻牌是8♥ 7♠ 5♠的特定例子。
根据胜率表格,这个翻牌面对大盲玩家有利。它将大盲玩家的范围从41.5%改进到50.33%,使他具有微弱优势。你的整体范围胜率从58.5%减少到49.67%,这意味着一般而言你应该玩得更小心,因为大盲玩家将会有许多高胜率牌,比如顺子、暗三条、两对和组合听牌。如果你选择在翻牌圈以较高频率持续下注,大盲玩家可以极高效地对你check-raise。如果你选择在翻牌圈随后check,大盲玩家可以开始在许多转牌圈和河牌圈激进地下注。即使你的真实牌A♦ A♣的胜率很高(70.83%),你通常也应该考虑被动地游戏,用许多可能在各种转牌面改进的牌随后check,使它们能够更轻松地跟注对手的下注。
因为A♦ A♣能够跟注几乎所有转牌圈下注,也可以高效地抓诈唬,你应该随后check。牌局的后续发展如下:

在这种场合A♦ A♣是一手极好的抓诈牌。所有听牌都错过,而你的底牌中没有任何红桃或黑桃,这使得对手更可能诈唬,因为你没有阻断各种诈唬牌(同花听牌)。
当然,记住所有的底牌对阵情况和范围对阵情况或者在打牌时做精确的胜率计算是不可能的。但是,胜率是扑克成功的关键。为了熟悉一些你将时常遇到的最常见局面,你必须花一些时间研究胜率计算器。
了解你自己的范围组成很重要,因为你范围中的每手牌必须以最有利可图的方式游戏。
期望值(EV)
EV是长期而言在给定情况下你预计平均将赢得或输掉多少。
EV = 长期期望值
从数学上说,EV是每个可能结果的概率乘以它们的绩效(收益或亏损)的总和。
EV = [%W * $W] – [%L * $R]
这里:
%W=你获胜的频率,即你的胜率。
$W = 你可以赢得多少钱。
%L= 你失败的频率,即100% – 你的胜率。
$R = 你为了采取行动必须用来冒险的资金。
t 如果这个公式的结果是个正数,那么玩法是正期望值(+EV)的,长期而言将赢钱。
t 如果这个公式的结果是个负数,那么玩法是负期望值(-EV)的,长期而言将输钱。
t 如果这个公式的结果是零,那么玩法是零期值(0EV)的,长期而言将不输不赢。
根据定义,弃牌的EV总是零。资金一旦进入底池就不再属于你。EV计算从你决定你的下一行动开始。因此,因为弃牌没有投入任何资金去冒险,弃牌的EV为零。
EV计算非常有用,因为它们决定了牌局应该如何游戏。如果牌手知道每个单独底池中每一行动的确切EV,游戏将非常简单,因为他们只需要总是选择最高EV的选项。
牌例
牌局类型:100美元买入网络3人Jackpot SNG比赛
筹码量:按钮玩家35BB,小盲玩家15BB,大盲玩家25BB
牌手数量:3人(无前注)
翻前:Hero在按钮位置拿着A♠ 5♠
Hero加注到2BB,小盲位置的常客玩家全压15BB。大盲玩家弃牌,轮到Hero做决定。
花一点时间,挨个分析EV公式的各部分。
对手是个常客玩家,因此你可以给他分配一个20%起手牌的标准全压范围。

底牌范围9:一个20%起手牌的标准小盲玩家全压范围
使用一种胜率计算器,你将看到你的A♠ 5♠对抗小盲玩家的范围具有43.31%胜率。
%W = 43.31%
你可以赢得SB玩家的15BB筹码和死钱(大盲注及你加注的2BB)。因此,
$W = 15 + 1 + 2 = 18BB
你输掉底池的频率是:
%L = 100% – 43.31% = 56.69%
你需要跟注的数目是:
$R = 13BB
将这些数据全部代入公式:
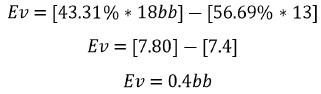
你决定用A ♠ 5♠ 跟注,因为它是EV更高的选择。当你跟注时,你有0.4BB的EV,而当你弃牌时,你是零EV。
赢率(Win Rate)
形象化EV的另一种方式是每百手牌赢得或输掉的大盲注(BB/100)。因为我们用大盲注计算EV,你只需要将EV乘以100。
扑克盈利应该通过长期结果来衡量。经常做出更好决定的能力允许最好的牌手长期盈利。他们反复采用EV最高的行动。
如我们在本例所见,每次都用A♠ 5♠跟注的牌手相比总是弃牌的牌手平均而言每百手多赚到40BB。
赢率 = 40BB/100
即使0.4BB似乎是个较小的风险回报率,但正是这种小优势,经过成千上万手牌后构成了世界级牌手和新手之间的差异。在漫长的扑克生涯中,这些小优势最终转化成为了数十万甚至数百万美元。
知道底牌对抗对手范围的胜率可以帮助我们预测EV和做出更好决定。
以底池大小为基准的EV
以底池的一部分来考虑EV往往是有益的:
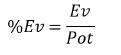
例子
底池有150美元,你被告知两种不同行动(A和B)的EV:
EV(A)= $75
EV(B)= $100
两种行动的相对于底池大小的EV是:
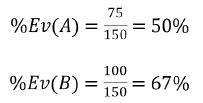
行动B相比行动A多拿到17%的底池,这使得它是绝对更好的行动。
弃牌赢率(FE)
弃牌赢率(Fold Equity)表示你因为对手对下注弃牌的可能性而注定赚到的额外赢率(Equity)。
弃牌赢率 = 对手弃牌的概率 * 对手的底牌赢率
总赢率(Total Equity) = 弃牌赢率(Fold Equity) + 底牌赢率(Hand Equity)
牌例
牌局类型:215美元买入网络扑克锦标赛
有效筹码量:100BB
牌手数量:9人(无前注)
翻前:Hero在CO位置拿着8♦ 7♦,并用它加注到2.5BB。后面玩家弃牌,大盲玩家用3♦ 3♥跟注。
翻牌圈:A♠ K♠ 5♣
大盲玩家check。Hero应该怎么做?
在这个例子中,大盲玩家的小对子具有71%胜率(底牌赢率)而Hero具有29%胜率。但是,如果你在翻牌圈下注,你可以指望对手在超过75%的时候放弃他的垃圾牌。因此,我们使用弃牌赢率公式可知:
弃牌赢率 = 75% * 71% = 53%
总赢率 = 53% + 29% = 29% = 82%
然而,术语弃牌赢率(Fold Equity)往往被用来简单地指代迫使某个牌手弃牌的可能性(即对手的弃牌率)。
牌例
牌局类型:109美元买入网络9人桌MTT锦标赛
有效筹码量:按钮玩家35BB,小盲玩家25BB,大盲玩家15BB
牌手数量:9人(12.5%前注)
翻前:(2.625BB) Hero在大盲位置拿着T♦ 5♣
按钮玩家加注到2BB。他是一个超激进的牌手,游戏很多牌但往往在遇到抵抗后放弃。小盲玩家弃牌,轮到Hero做决定。
你的牌非常糟糕,而且对抗常客玩家你通常会弃牌。但是,你知道对手在按钮位置游戏太多牌。因为一个宽范围更难防范再加注,你猜测如果你在这种场合全压对手可能过度弃牌(over-fold)。那么,为了使T♦ 5♣全压有利可图你需要多少弃牌率?
为了回答问题,你可以使用EV公式,使EV = 0,对手的弃牌率 = FE。
EV = 对手弃牌的EV * 对手的弃牌率 + 对手跟注的EV * 对手的跟注率 + 被对手再加注的EV * 对手的再加注率
现在分析这个公式的每个部分。
当对手弃牌时,你得到整个底池:
弃牌的EV = 初始底池大小 = 盲注及前注 + 对手的加注额 = 4.625BB
因为你全压,对手无法对你再加注。因此,
被对手再加注的EV * 对手的再加注率 = 0
且
对手的跟注率 = 1 – FE
如果你被跟注,你将游戏一个总共31.625BB的底池。你要拿额外14BB冒险,而且你预计T♦ 5♣对抗对手的跟注范围将有约31%胜率。
对手跟注的EV = 底池大小 * 我们的底牌赢率 – 风险额
对手跟注的EV = 31.625 * 0.31 – 14 = -4.19BB
将所有数据代入公式:
0 = 对手弃牌的EV * FE + 对手跟注的EV * (1 – FE)
0 = 4.625 * FE + (-4.19) * (1 – FE)
0 = 4.625FE – 4.19 + 4.19FE
0 = 8.82FE – 4.19
8.82FE = 4.51
FE = 4.51 / 8.82 = 0.51 = 51%
为了使T♦ 5♣全压有利可图你需要至少51%的弃牌率。
你预计对手在按钮位置用约60%起手牌率先加注,并用28.8%起手牌跟注大盲位置全压(底牌范围11)。

底牌范围10:包括60%起手牌的按钮位置率先加注范围
按钮玩家的跟注频率:
跟注率 = 跟注频率 / 率先加注频率 = 28.8 / 60 = 0.48 = 48%
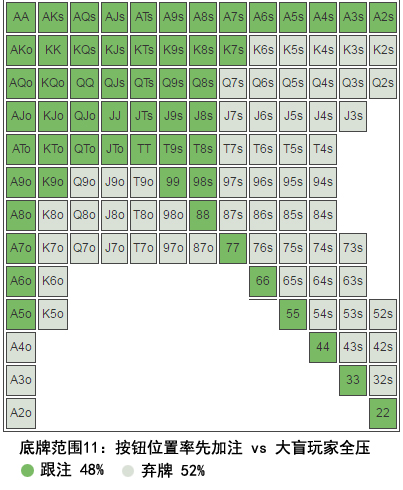
按钮玩家的弃牌率是:
按钮玩家弃牌率 = 100% – 跟注率 = 100% – 48% = 52%
Hero需要的最低弃牌率是51%,而他有52%弃牌率。因此,用T♦ 5♣全压是(勉强)有利可图的玩法。
扑克反水-德州扑克反水-博狗扑克反水-蜗牛扑克反水-扑克之星反水-联众扑克反水-天龙扑克反水