Grinder手册
网络无限德州扑克六人桌常规局完全教程
Grinder Manual
A Complete Course in Online No Limit Holdem 6-Max Cash Games

此书于2016年初出版,部分内容或已过时,仅供参考。
第九章 组合与阻断牌
我们目前为止做了一些间歇性的数学工作。我讲授了两个最基本过程:计算需要的胜率和计算需要的弃牌赢率,但目前为止我避开了扑克中最有用的数学方法:理解如何利用组合和阻断牌去帮助决策制定。
我们将在本章首先介绍“组合”这个概念,然后转入阻断牌。
组合(Combo)是52张牌的牌堆中任意两张牌的组合,它构成了德州扑克中的确切起手牌。
A♣ A♥是一个组合,A♥ A♠也是一个组合。AA是所有包括两张A的组合群(combo group)的名称。我们说A♣ A♥是AA的一个组合。
在我们学习如何应用组合到每天的扑克思维之前,记住这三种翻前组合群类型和每种组合群包括多少单独的组合很重要。
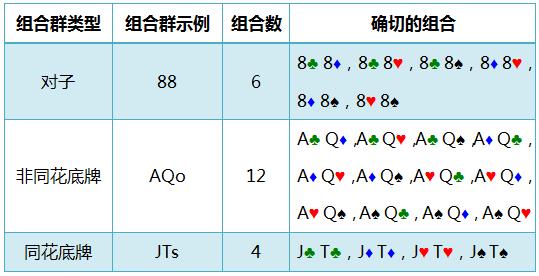
图47-底牌与组合
注意,8♣ 8♦是和8♦ 8♣是完全相同的组合。我们只关心哪两张牌构成了起手牌,而不在乎它们发出的顺序。Hero翻前可能发到的组合有1326种,每种组合和其他组合发出的概率是相同的。但是,当我们开始把组合归合到我们通常所说的“起手牌”群组(比如KK、32o或45s)时,我们看到这些牌发出的频率是不同的。一手牌的组合有多丰富是发到那手牌有多容易的衡量指标。一名牌手翻前范围的每一个口袋对子有6种组合,但他的每一种非对子底牌有16种组合。发到一个非对子底牌相比发到一个对子容易两倍多。
假设在某个怪异扑克宇宙的某个怪异对手有一个只包括AA和72的按钮位置率先加注范围,他将只有6 / (6 + 16) = 27%的时候拿着AA。
这表明起手牌的自然分布是不均匀的。理解它们不均匀的发出方式使我们对一个牌手多可能拿到其范围的某个部分或当Hero范围包括特定起手时有多平衡或不平衡有更好的感觉。我们可以为了两个目的利用组合:
l 推测我们的对手到一些范围,然后判断我们对抗那些范围应该怎么做。
l 构建我们自己的范围,从而我们能够致力于为特定局面制定良好的长期策略。
在关于3bet的下一章,我们将利用组合构建我们自己的范围。现在我们来看一些利用组合评估对手范围的实例。
9.1 翻前利用组合
下面的牌局说明了一个我们的解决方案与讨论应对3bet的第十一章更接近的牌局。我们将把这个场合作为良好的组合如何能帮助我们避免一个极常见陷阱的好例子。
一般而言,如果Hero在按钮玩家对抗大盲玩家的场合4bet,他将打算跟注全压。假设为了讨论的缘故,我们知道对手对我们的4bet全压的范围恰好是KK+和AK。如果对手不用许多差牌跟注,这可能使得Hero的4bet是有点问题的,但我们暂且忽略这一点。
一些学生现在会问以下问题:
“用QQ跟注全压怎么可能是+EV的?如果对手只用KK、AA和AK全压,那么Hero岂不是要么五五开要么被击溃?”
好的,在我们进一步讨论之前:Hero在这种场合真正需要考虑的是什么?对了,他跟注需要的胜率(RE)。如果Hero不考虑这一点,那么他将开始错误的分析。这是一个终止行动场合(参见第七章)。
我们知道RE = ATC / (ATC + TP),在本例中是:76 / (76 + 124.5) = 37.9%。
我们需要抛弃的危险假定是:Hero为了跟注需要在一半或更多时候胜过对手。
既然我们知道了我们的RE,我们需要计算我们对抗对手范围的胜率。我们将首先使用一种胜率计算器计算胜率,然后我们用组合来解释为什么计算结果是那样。
胜率计算器告诉我们,Hero的QQ对抗范围{KK+,AK}的胜率是39.9%,这确实是一个舒服的跟注,但为什么会这样?
诚然,Hero对抗AK的胜率接近50%,而对抗KK和AA的胜率显著减少。我的学生声称Hero“要么五五开要么被击溃”是接近正确的。在这里Hero的胜率足够跟注是对抗的组合偏离击溃我们的大对子而偏向我们稍占上风的AK的一个直接结果。
应用我们目前学到的组合知识,我们知道非对子底牌有16种组合(12种非同花组合和4种同花组合),而一种口袋对子只有6种组合。这意味着对手的范围包括16种我们略占优势的组合(AK),而只有12种击溃我们的组合(KK和AA)。这就是我们在这里有40%胜率的原因。
这里的一种错误想法是,因为有两种结果,一个中性结果和一个坏结果,胜率情况必定很糟糕。无法意识到这两种结果出现频率的巨大差距被我叫做均等机会谬论。
均等机会谬论(Equal Chance Fallacy)是认为因为只有两个选择,那些选择的可能性是均等的。
当我离开房间出门跑步几分钟时,我们可以确定两个可能的结果。肯定两个事件之一将会发生:
l A:我将被贪婪的海鸥啄死。
l B:我没被贪婪的海鸥啄死。
我几乎完全确定B事件而非A事件将会发生,而那也是为何我可以毫无自杀倾向的出门跑步。用扑克语言来说,B组合的数量远多于A组合的数量。
可能显而易见,甚至说出来是侮辱你的智商,但我想要用这个荒谬的海鸥案例驱散一个扑克思维中真正最常犯的错误,也就是——忽略组合和它们构成一个范围的一部分的可能性如何去比较另一个范围。
接下来我们考虑我们可以如何在翻后利用组合确定怎样对抗对手的范围。
扑克反水-德州扑克反水-博狗扑克反水-蜗牛扑克反水-扑克之星反水-联众扑克反水-天龙扑克反水