蜗牛扑克allnew官网,蜗牛扑克allnewpoker官网,蜗牛扑克allnewpoker国际场,allnewpoker官网下载,蜗牛扑克网站,蜗牛扑克下载——(allnewpuke.com)

当我们使用经典统计方法时,我们可以求出一个极大似然估计量。使用同样的方法,我们可以定义-1bb/100手是在给定假设条件下所求出的极大似然估计值。当然,这些假设不是完全真实的:牌手们的可能赢率是接近于连续的。不过,如果我们将其设为连续函数,并且做一些更复杂的数学计算,我们会发现其分布与目前的分布是相当接近的。而这个方法的关键含义是因为盈利玩家的相对稀缺性,我们假想的这位玩家是一位运气非常好的输钱玩家和有稳定赢率的盈利玩家的可能性几乎是相当的。
如果我们考虑一个有着更高赢率的选手(假设为5bb/100手),我们可以更明显地观察到这一点。经典统计方法会使得我们设定一个极大似然估计量为5bb/100手,因为它考虑到所有赢率产生的可能性是相当的(因为在经典统计方法中我们假定我们对赢率的分布没有其他附加信息)。然而,用5bb/100手的赢率重新进行上述计算后,我们发现:
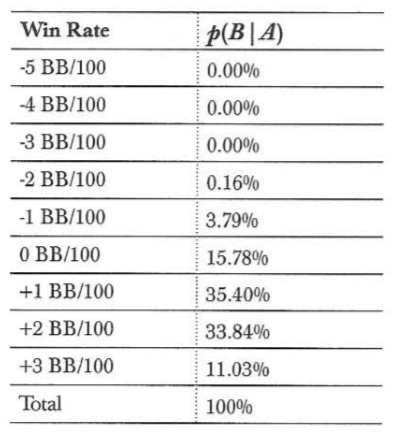
我们可以看到这里,我们的玩家严重偏向于一个盈利的玩家,并且有很大可能性确实是这样。但是,5bb/100手的玩家并不存在于分布总体中,贝叶斯定理更可能将其调整为赢率水平在前10%的玩家。
收集更多的数据很自然地会使得所观察到的赢率向贝叶斯估计量汇集——一个牌手越经常出现这样的赢率,他的真实赢率就越可能与之相等。而我们如果对十万手牌的样本重新进行上述计算,我们就有:
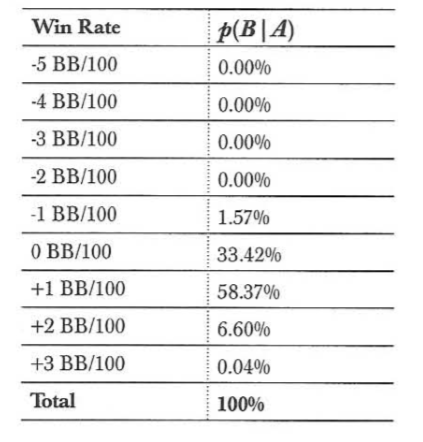
通过这样一个样本量,我们可以对观察到的样本与现实匹配更有信心,即便在真实的分布下只有10%的牌手赢率超过1bb/100手。
关于经典统计量(有时又被称为频率统计量)与贝叶斯统计量之间的分歧是没有意义的。而争论的中心(大概)是贝叶斯方法的想法是总体参数应该被设定为一个概率分布。贝叶斯方法估计一个先验分布,观察一个样本,之后通过新的信息调整这个先验分布。而频率估计量拒绝这种方法,更倾向于认为总体变量是固定的,不变的定值,即使我们不知道它们的确切值。我们更倾向于贝叶斯方法的观点,因为它在扑克中是非常实用的。
我们在这边使用的方法还不是贝叶斯统计量技术的全部功能,而只是贝叶斯分析技术的一个简化技术,为了使得我们的观点被更清晰地阐述。如果你想得到更多的关于贝叶斯方法与经典统计方法之间的区别,我们建议你阅读一些统计学方面的进阶的论文,特别是那些把着重点放在估计与贝叶斯方法的。
从这个分析中兴起的一个话题是对均值回归的思想。假设你从一个样本中抽取一个少量的观测值的赢率。这里的想法在于被观测到的高于目前均值的样本会在将来变低(如果你以后继续做这个测试的话),而现在那些低于平均值的样本会倾向于有更好的表现。这并不是因为有任何统计方面的“趋平”使得过去的样本与其未来值有影响——其实他们都是相互独立的。在这里运用的理论是如果你对总体的均值有一个高估,那么你对其期望值也高估了;而如果你低估了总体的均值,那么你对其期望值也高估了。最终,你会对每一个牌手的估计都会略微向总体均值偏移——而最佳的预测也就是总体均值混合一些观察到的样本值。我们可以看到这在外面假想的牌手的贝叶斯统计量中——经过16900手后,他的经调整的赢率预测仍然很受总体分布的影响,最终把他的赢率拉低到接近于-1bb/100手的数据。
畅玩线上德州扑克,只需简单步骤就能在Bodog博狗畅玩扑克,
博狗扑克官方网址 博狗扑克网址:
http://www.bogoupoker.com
扑克反水-德州扑克反水-博狗扑克反水-蜗牛扑克反水-扑克之星反水-联众扑克反水-天龙扑克反水












